Accelerating a Signal Processing Algorithm with TornadoVM: The Implementation
Introduction
In the first post of this series, we have introduced one algorithm, Period Search, that is central to the processing of photometric data acquired by the Gaia mission when studying variable stellar objects.The reader not familiar with those astronomical concepts should start by reading the introduction article before the present one.
In that post, we will report on the steps we took to accelerate the PeriodSearch algorithm with GPU. that relies on the computation of several sums of sines and cosines for a large number (approx. 600,000) of frequencies.
When it comes to GPU parallelization, the computation of the frequencygram benefits from the independence of the frequencies. It is easy to adopt an embarrassingly parallel approach, letting each thread compute a single frequency.
The local maxima selection requires each thread in charge of a frequency to have access to its predecessor and successor, which is less easy than it seems on certain GPU architectures. On NVidia chips, for example, it is easy to access registers of threads in the same warp (group of 32 threads) but going past those boundaries requires using shared memory, which is slower than registers for the main computation.
The identification of the K best frequencies requires ideally to have a vision of the whole frequencygram, which is not an ideal scenario for GPUs. This step is however close to a classical reduction operation and could be handled in the same way. Some algorithms are efficient to select the maximum or to calculate aggregate hierarchically. However here the limitation derives from our need to select more than one frequency, but to select the K best ones, which limits the parallelization possibilities.
The refinement step is similar to the initial algorithm, but with a different number of frequencies to examine, this number depending on the scenario parameters. To be noted here that this step needs to be performed in double precision, which is not what classical GPUs are strong at. We therefore either need to use dedicated GPUs like Nvidia A100, or to have sub-optimal performance.
Parallelizing with TornadoVM
With all these considerations in mind, we used TornadoVM to evaluate multiple strategies utilizing both GPU and CPU computation. The challenge here is to choose the best strategy considering that:
- GPUs are pure SIMD architectures, meaning that in an optimal scenario, the algorithm shall have the exact same execution, instruction by instruction, over much data.
- In the general case, GPU and CPU don’t share the same memory, which means that transfers are necessary back and forth and can be costly. Transferring the time series represents little data, but the frequencygram is much heavier and could stay in the GPU memory if we don’t want to export the full frequencygram.
- GPUs are meant to manipulate single precision floating point numbers or half precision for the graphics and artificial intelligence applications. We may need double precision, which is generally handled by far less computation units, if any.
- GPU occupancy should be maximized, which is a classical computation – communication overlap issue that has been an active concern since PVM and MPI. Nvidia chips allow, however, transmissions from the CPU to the GPU to happen in parallel of computation on the GPU and in parallel of communication in the reverse direction.
TornadoVM, developed by University of Manchester and improved within the AERO project, provides an API and an execution framework that abstracts the hardware layers, allowing the same Java code to be parallelized and executed on heterogeneous hardware, from Nvidia GPUs to intel GPUs and even CPUs through the PoCL language. It seems to suit our scenario perfectly since the Gaia pipeline is written in Java and since we dispose of multiple machines, some of them running Intel GPUs and some running Nvidia GPUs.
Our first attempt, as a proof of concept, has been to annotate our loops with the @Parallel annotation. This approach is easy and provides a first level of parallelization.
The performance was not much improved because the frequencygram calculation algorithm on CPU had been optimized by minimizing the number of invocations of the trigonometric functions. Instead of calculating the sines and cosines for all frequencies independently, we calculate the sine and cosine of the initial frequency and the ones of the frequency increment, then only use expressions such as sin(f + δf) = sin(f)cos(δf) + cos(f)sin(δf). This improves performance but introduces dependencies between the frequencies which strongly limits parallel computation opportunities. On the GPU we had to use the original algorithm and double precision trigonometric functions are slow.
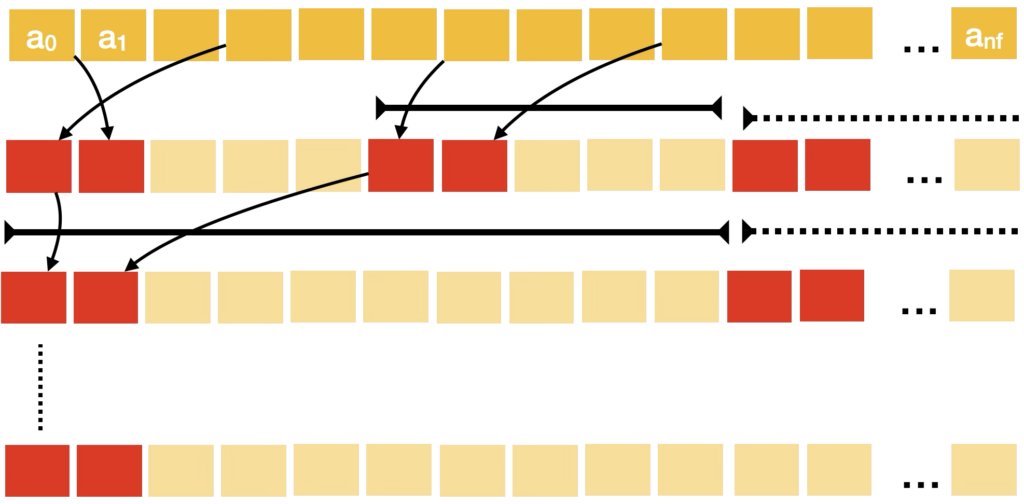
When it comes to maxima selection and other reduction-like mechanisms, the algorithms will let a number T of GPU threads work in blocks, selecting the best K frequencies among themselves, then combine two blocks together repeatedly until we only have one list, as shown on the Figure below. If this algorithm is hierarchical and involves a logarithmic number of steps, during all these steps, a larger and larger number of threads, represented in light yellow, are unoccupied, which leads to an under-utilization of resources.
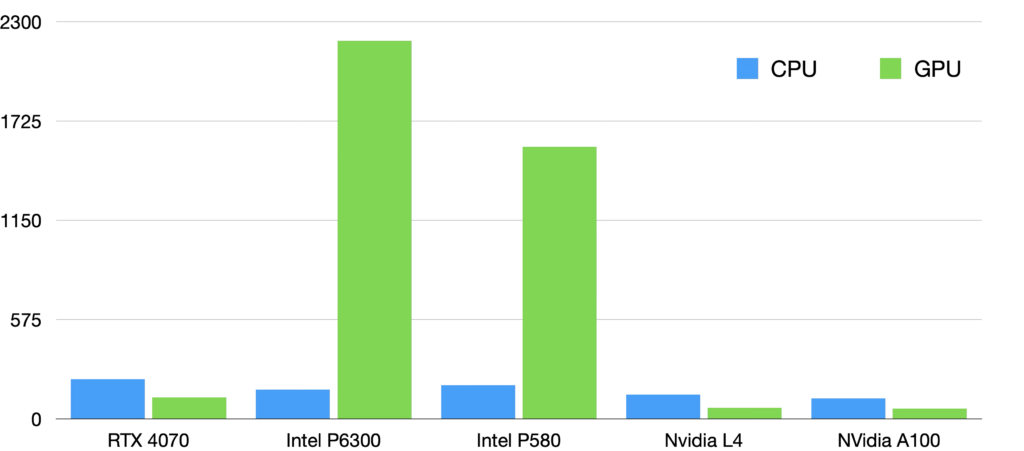
We then tried to use the Kernel API to perform the whole computation on the GPU. The GPU receives a time series as three arrays (times, observations, errors) and produces the final metrics, the K identified best frequencies refined to double precision and the final statistics. This approach leads to some moderate speedups on some of our machines, mostly the ones with a modern NVidia GPU, from consumer grade GPU (RTX 4070) to A100. However, on the legacy machines with a Intel GPUs, this leads to a serious performance degradation as represented on the graph below.
We then tried a second approach, using the Kernel API, that consists of offloading the whole computation to the GPU with the following steps:
- Transfer the time series and problem parameters to GPU.
- Spawn GPU threads that each calculate the amplitude of a single frequency in single precision (float).
- Transfer back the whole frequencygram to the CPU.
- On the CPU, filter out the frequencies that are not local maxima, insert the remaining ones in a Max-heap structure with a score equal to the amplitude.
- Extract the K best frequencies from the Max-heap and list the frequencies to re-evaluate in their vicinity in double precision
- Send those new frequencies to the GPU to be computed in double precision this time. This step can be handled by the CPU too depending on the hardware characteristics (e.g. NVidia A100 vs. legacy GPU)
- Transfer back the new frequencies and select the best refined samples.
- Calculate on CPU the global statistics.
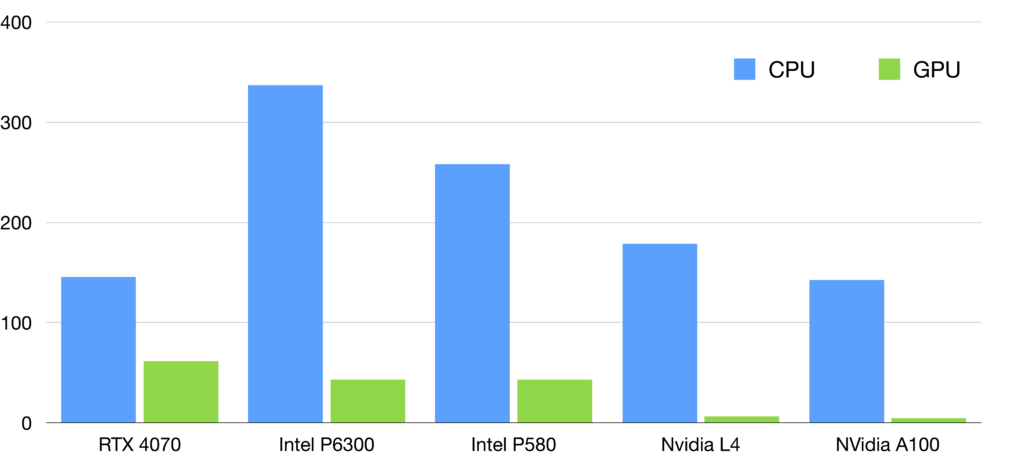
This algorithm showed an encouraging performance gain, but we noticed that the GPU utilization was poor. Since the CPU takes care of several steps, the strategy of processing one time series after the other was ineffective since we cannot control the communication vs. computation overlap. We therefore chose to send not only one time series at a time to the GPU, but as many as possible in order to reach the limits coming from memory allocation, which represents batches of 800 time series. This led to an important performance increase, as shown on the graph below.
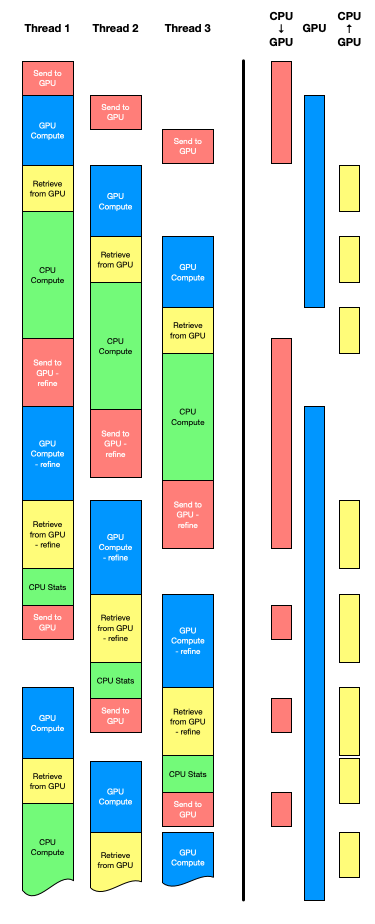
Starting from there, we modified our algorithm to allow multiple threads to run in parallel. The goal is to have one thread send data to the GPU while the GPU is busy processing another thread’s batch, and yet another one is transferring back data, and a last one is calculating on the CPU. In other words, don’t let any resource be unutilized, as represented on the diagram below. The challenge for this scenario is memory management, both on the CPU and GPU, since the limits must be respected, and each thread does not know what the other threads or processes are requesting. A call to the driver to know the volume of free memory before starting a new thread would be welcome but is not available from Java at least.
The diagram below represents, on the left side, how three CPU threads launching batches would organize themselves, considering that only one thread at a time can use the transfer in one direction or the GPU computation. A single CPU can run multiple computation threads in parallel without much disruption if we stay below the number of cores. We can notice that the exclusive access to the three shared resources introduce some pauses in threads occasionally.
The right part of the graphic shows the timeline of the usage of the two communication directions and of the GPU. The goal is to maximize the GPU usage and if, on that small example, we may achieve a good performance overall, inactivity periods like the one in the middle of the timeline may happen because no data is present on the GPU to be processed. This problem is not trivial, and heuristics may be imagined to reduce down periods to the minimum, but they are beyond this work for now.
As a last bit of optimization, we used TornadoVM’s capability to load PTX kernels to develop Cuda kernels for the Nvidia platform and run it through Tornado. This allows small optimizations like the use of the sincospi() function that calculates in one call the sine and cosine of a variable multiplied by pi, providing us with a slight performance gain. However we must fall back on the OpenCL implementation for the Intel machines, which is not ideal from a development standpoint, since it leads to some code duplication. It is however very good that TornadoVM allows such operation that optimizes performance.
Conclusions
The process of adapting our Period Search algorithm to an efficient GPU implementation has required experimentation before achieving a fair speedup. If the present version is not perfect, its performance shall allow to push the scientific analysis one step further with longer time series. We will continue experimenting to improve the hotspots of the algorithm, even though there is a limit to optimization. There are natural dependencies between successive steps of the algorithm and sometimes, optimizing one region of the code requires introducing costly modifications in other regions to adapt and prepare the data.
We learned several lessons in that process. First of all, achieving speedup with GPU consists in searching for some limits. Those limits may be the load of the graphical processor, the memory, or the bus capacity in case of large data chunks. At least one of those factors should be at its maximum and none should be under-utilized. Reaching those limits may require having multiple CPU threads accessing concurrently the GPU to better ensure a proper overlap between communication and computation. The CPU shall also be utilized for more than orchestration, and finding the right balance between what is executed where requires some experimentation, especially when the communication is not instantaneous.
Overall, TornadoVM provides an API that allows the developer to work at different depths, from a quick and easy prototype to more detailed implementations closer to the vendor APIs. Performance-wise, TornadoVM may get close to a native implementation but can also be slower, which is expected since it is not a compiler by itself. Nevertheless, TornadoVM abstracts the heterogeneity of the execution platforms, allowing to reuse the code across different machines with different architectures and is therefore well adapted to several scenarios, including a grid-like or cloud-based execution.
